Navigation:
Last Update:
12.02.2017
Ergänzung zur Berechnung
Testlauf auf facebook:
Schiffs-Barometer am Chiemsee
Die korrekte Kalibrierung auf den relativen Luftdruck
Von Dipl.-Ing. Tilo Klesper
Alles begann, als ich neulich dieses alte Barometer bekam. Ich wollte es auf
den neuen Ort kalibrieren. Aber es hatte diese fremde Skala, auf der keine
Angabe über die fremde Einheit angegeben war. Also begann ich zu recherchieren.
Während ich mich durch die Literatur kämpfte, fand ich das Thema immer spannender.
Und weil die einzelnen Artikel, insbesondere auch in der Wikipedia,
mancherlei Fehler und Widersprüche enthielten, schrieb ich für mich selber eine
Zusammenfassung. Daraus entstand letztlich der folgende Artikel.
HINWEIS: Dieser Artikel ist noch nicht ganz fertig (Status: In Bearbeitung).
Ich warte derzeit noch auf das eine oder andere Feedback der Profis, bei denen
ich zwecks fachlicher Beurteilung angefragt habe.
Mit der Freigabe der endgültigen Version wird dieser Hinweis entfernt.
05.09.2015 (Erster Entwurf)
(...)
10.01.2017 (Bildnachweis)
(...)
06.02.2017 (Korrekturen zur Wetterstation Chieming)
11.02.2017 (Korrektur wesentlicher Fehler in den Berechnungen)
12.02.2017 (Ergänzung Gegenrechnung auf Höhe der Wetterstation)
Schiffs-Barometer am Chiemsee

Auf dieser Seite finden Sie neben allgemeinen Informationen zu Barometern spezielle Hinweise zu den physikalischen Einheiten, zur Kalibrierung auf den auf Meereshöhe reduzierten Luftdruck sowie die Besonderheiten der englischen Skala. Bei der Kalibrierung wird neben der Theorie auch die spezielle meteorologische Situation am Chiemsee berücksichtigt.
Direkt zu:
- Allgemeines
- Physikalische Einheiten
- Die englische Barometer-Skala
- Auf Meereshöhe reduzierter Luftdruck
- Praxis (nicht nur) für den Chiemsee
- Wetterdaten Chieming
- Quellennachweis und Links
Allgemeines
Barometer messen den lokalen Luftdruck (genau: den statischen Absolut-Luftdruck) und zeigen diesen in bestimmten physikalischen Einheiten auf einer Skala oder digital an. Auf unseren Schiffen sind üblicherweise sog. Dosenbarometer, auch Aneroidbarometer genannt, installiert. Sehr vereinfacht gesagt, drückt der Luftdruck eine spezielle Unterdruck-Blechdose mehr oder weniger zusammen. Die Verformung dieser Druckdose wird mechanisch mit einem Zeiger auf einer meist runden Skala angezeigt. Bei der technischen Ausführung der Druckdose gibt es erhebliche qualitative Unterschiede. Hochwertige Barometer haben eine Druckdose aus verschiedenen Metall-Legierungen, die eine Temperatur-Kompensation sicherstellen. Daraus resultieren u.a. auch die erheblichen Preisunterschiede.
 Eine besondere Ausprägung des Schiffs-Barometers ist der mechanische Barograph.
Er zeichnet den
Verlauf des Luftdrucks (Barogramm) auf einem Skalenpapier auf,
das auf eine stetig rotierende Trommel (1/24h) gespannt ist. Der Aufbau ist wesentlich
komplexer, es sind mehrere Aneroid-Dosen hintereinander verbaut und die
Mechanik ist ölgedämpft, um auch im Wellengang eine verlässliche Aufzeichnung
zu gewährleisten. Die physikalischen Prinzipien, die im folgenden vorgestellt
werden, sind trotz aller mechanischen Finessen dieselben wie bei einem einfachen
Barometer.
Eine besondere Ausprägung des Schiffs-Barometers ist der mechanische Barograph.
Er zeichnet den
Verlauf des Luftdrucks (Barogramm) auf einem Skalenpapier auf,
das auf eine stetig rotierende Trommel (1/24h) gespannt ist. Der Aufbau ist wesentlich
komplexer, es sind mehrere Aneroid-Dosen hintereinander verbaut und die
Mechanik ist ölgedämpft, um auch im Wellengang eine verlässliche Aufzeichnung
zu gewährleisten. Die physikalischen Prinzipien, die im folgenden vorgestellt
werden, sind trotz aller mechanischen Finessen dieselben wie bei einem einfachen
Barometer.
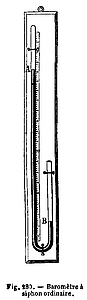 Frühere, historische Instrumente und moderne elektronische Geräte nutzen
andere Techniken. Bekannt sind vor allem das Quecksilber-Barometer, dessen erster
Versuchsaufbau
1643 von dem Forscher Evangelista Torricelli stammte. Genau genommen
wiederholte dieser die Experimente mit Wasser-Röhren und die Suche nach der
physikalischen Erklärung, die ab 1630 von
Galileo Galilei, Gasparo Berti, Giovanni Battista Baliani und anderen Forschern
vorgenommen wurden. Torricelli ersetzte das Wasser durch Quecksilber, das eine
wesentlich höhere Dichte hat. Die Länge der Röhre reduzierte sich dadurch von über 10 m
(Normaldruck = 10,3 m Wassersäule) auf ca. 80 cm (Normaldruck = 760 mmHg, auf deutsch
Millimeter Quecksilbersäule). Glaubte Galileo noch an die "Kraft des Vakuums",
postulierte Torricelli eine Kraft, ausgeübt durch das Gewicht der Luft.
Frühere, historische Instrumente und moderne elektronische Geräte nutzen
andere Techniken. Bekannt sind vor allem das Quecksilber-Barometer, dessen erster
Versuchsaufbau
1643 von dem Forscher Evangelista Torricelli stammte. Genau genommen
wiederholte dieser die Experimente mit Wasser-Röhren und die Suche nach der
physikalischen Erklärung, die ab 1630 von
Galileo Galilei, Gasparo Berti, Giovanni Battista Baliani und anderen Forschern
vorgenommen wurden. Torricelli ersetzte das Wasser durch Quecksilber, das eine
wesentlich höhere Dichte hat. Die Länge der Röhre reduzierte sich dadurch von über 10 m
(Normaldruck = 10,3 m Wassersäule) auf ca. 80 cm (Normaldruck = 760 mmHg, auf deutsch
Millimeter Quecksilbersäule). Glaubte Galileo noch an die "Kraft des Vakuums",
postulierte Torricelli eine Kraft, ausgeübt durch das Gewicht der Luft.
Ab 1646 perfektionierte ein gewisser Blaise Pascal1) die Experimente und die neuartige Theorie vom Druck der Luft anstatt der Kraft des Vakuums. 1648 konnte er mit Hilfe seines Schwagers Florin Perier die Theorie experimentell nachweisen und erstmals die Abnahme des Luftdrucks mit der Höhe aufzeigen.
Der französische Forscher René Descartes, der schon 1631 ein ähnliches Experiment beschrieben hatte und schon früh eine Abnahme des Luftdrucks mit der Höhe voraussagte, perfektionierte ebenfalls Torricellis Quecksilber-Apparatur, indem er eine Papierskala an der Glasröhre anbrachte. Diese Apparatur konnte erstmals zum Messen verwendet werden. Und ab ca. 1665 wurden diese Apparaturen von dem irischen Forscher Sir Robert Boyle, der die endgültige, gebogene Form des Rohrs als sog. "Siphon-Rohr" erfand, "Barometer" genannt. Dieser Name leitet sich aus den griechischen Begriffen báros (Schwere, Gewicht) und metreín (messen) ab.
 Auf Schiffen wurden früher neben den Quecksilber-Barometern auch
die dekorativen, sog. "Goethe-Barometer" zur
Vorhersage der Wetterentwicklung, vor allem aber zur Vorhersage von Stürmen
benutzt. Diese Glas-Gefäße (s. Bild rechts) wurden daher auch als Sturmglas
oder Wetterglas bezeichnet. Goethe war jedoch nicht der Erfinder,
vielmehr war es schon vor Galileo im
niederländischen Raum verbreitet. (Hatte Galileo nicht auch sein Teleskop von einem
Holländer "kopiert"?) Bekannt waren im 17. Jh. vor allem die Instrumente des
Holländers G. de Donckere, die nach diesem auch Donnerflaschen genannt wurden.
Und weil später, im 19. Jh., die Glasbläser in Lüttich (Liège) diese
Glasgefäße in Serie herstellten, werden diese auch "Baromètre Liégeois"
2) genannt.
Auf Schiffen wurden früher neben den Quecksilber-Barometern auch
die dekorativen, sog. "Goethe-Barometer" zur
Vorhersage der Wetterentwicklung, vor allem aber zur Vorhersage von Stürmen
benutzt. Diese Glas-Gefäße (s. Bild rechts) wurden daher auch als Sturmglas
oder Wetterglas bezeichnet. Goethe war jedoch nicht der Erfinder,
vielmehr war es schon vor Galileo im
niederländischen Raum verbreitet. (Hatte Galileo nicht auch sein Teleskop von einem
Holländer "kopiert"?) Bekannt waren im 17. Jh. vor allem die Instrumente des
Holländers G. de Donckere, die nach diesem auch Donnerflaschen genannt wurden.
Und weil später, im 19. Jh., die Glasbläser in Lüttich (Liège) diese
Glasgefäße in Serie herstellten, werden diese auch "Baromètre Liégeois"
2) genannt.
Ab den 1990er-Jahren werden elektronische Wetterstationen, Armbanduhren, Aerometer, GPS-Geräte und neuerdings auch Smartphones mit Halbleiter-Sensoren (Microelectromechanical systems, MEMS) und piezo-elektrischen Sensoren gebaut.
Die eigentliche Messtechnik ist jedoch für diesen Artikel nur nebensächlich interessant, denn hier geht es um ein anderes Thema: Die meteorologisch korrekte Verwendung von Barometern auf dem Chiemsee. Oder kurz gesagt: Um die korrekte Kalibrierung (oft auch Justierung genannt, in der Google-Suche wird auch Einstellung als Suchbegriff genutzt).
Daher folgt jetzt ein bisschen Theorie.
Bekanntlich nimmt der Luftdruck mit zunehmender Höhe ab. Der Normaldruck gilt für Meereshöhe (Normal-Null, NN). Der Chiemsee liegt ca. 518,2 m über NN. Daher zeigen unsere Schiffs-Barometer hier einen geringeren Luftdruck an als die Wetterkarten. Jedenfalls, solange die Barometer nicht entsprechend kalibriert sind. Wetterdienste geben Messdaten, Berichte und Vorhersagen auf der Grundlage des normalisierten, sog. auf Meereshöhe reduzierten Luftdrucks, wieder. Dieser wird auch als "relativer Luftdruck" bezeichnet. Nur so lassen sich Vorhersagen, insb. über den zu erwartenden Wind, auch für Landgebiete mit ihren individuellen Höhen berechnen. Und Wetterkarten sinnvoll darstellen. Alle Isobaren-Karten werden daher mit dem relativen Luftdruck, also dem auf Meereshöhe umgerechneten Luftdruck erstellt.
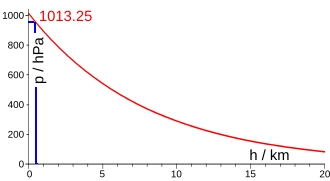 Der Luftdruck in einer bestimmten Höhe hängt im wesentlichen von den Parametern
Luftdichte,
Temperatur und Luftfeuchte ab. Dazu kommen vernachlässigbare Parameter wie der Breitengrad.
Das Bild rechts zeigt den Verlauf nach einer sog. "Höhenformel".
(Verwirrenderweise gibt es verschiedene Höhenformeln, die in der Literatur oft
gleichermaßen als Barometrische Höhenformel bezeichnet werden. Im folgenden
werden wir uns das genauer anschauen.) An dieser Stelle interessiert erst einmal nur
die Intention dieses Artikels:
Über die ergänzte blaue Linie im Graph können wir die Korrelation zwischen der
Höhe des Chiemsees und dem lokalen, absoluten Luftdruck erkennen und grob ablesen.
Damit ist rein grafisch der Inhalt dieses Artikels ausgedrückt.
Der Luftdruck in einer bestimmten Höhe hängt im wesentlichen von den Parametern
Luftdichte,
Temperatur und Luftfeuchte ab. Dazu kommen vernachlässigbare Parameter wie der Breitengrad.
Das Bild rechts zeigt den Verlauf nach einer sog. "Höhenformel".
(Verwirrenderweise gibt es verschiedene Höhenformeln, die in der Literatur oft
gleichermaßen als Barometrische Höhenformel bezeichnet werden. Im folgenden
werden wir uns das genauer anschauen.) An dieser Stelle interessiert erst einmal nur
die Intention dieses Artikels:
Über die ergänzte blaue Linie im Graph können wir die Korrelation zwischen der
Höhe des Chiemsees und dem lokalen, absoluten Luftdruck erkennen und grob ablesen.
Damit ist rein grafisch der Inhalt dieses Artikels ausgedrückt.
In diesem Artikel zeigen wir auf, wie wir Barometer am Chiemsee möglichst exakt auf die Anzeige des relativen, also auf den auf Meereshöhe reduzierten Luftdruck kalibrieren bzw. diesen ermitteln.
Dabei geben wir nicht einfach nur die Zusammenfassung der Literatur und der üblichen Rechenformeln wieder, sondern beziehen auch die spezielle metereologische Situation am Chiemsee mit ein.
Beginnen wir mit den einfachen Grundlagen.
Physikalische Einheiten
Die aktuelle, internationale Einheit (SI-Einheit) für den Luftdruck ist das Pascal (Pa). Die Einführung begann in der Bundesrepublik Deutschland ab 1970, in Österreich ab 1973, in der DDR ab 1974 und in der Schweiz ab 1978. In Deutschland und Österreich ist zusätzlich die frühere Einheit "Bar" (bar) zugelassen (Umrechnung: 1 bar = 105 Pa). In Wetterkarten und auf den Barometer-Anzeigen wird der Luftdruck allerdings nicht in Pascal (Pa), sondern in Hekto-Pascal (hPa) dargestellt. Der Grund dafür ist die einfachere Umrechnung zwischen alter und neuer Einheit: 1.000 hPa = 1.000 mbar.
Vor der Einführung der SI-Einheit Pascal (und danach übergangsweise bis 1977) gab es neben dem Bar noch die "Physikalische Atmosphäre" (atm) und die "Technische Atmosphäre" (at) als offizielle Standardeinheiten. Die Physikalische Atmosphäre geht zurück auf die historische Technik der Luftdruckmessung mit den damaligen Quecksilber-Barometern. Das Quecksilber zeigte den Luftdruck in einem Glasröhrchen auf einer metrischen Skala an. Die Einheit war entsprechend in "Millimeter Quecksilbersäule" (mm Hg) definiert. Nach dem maßgeblichen Erfinder dieser Technik wurde diese Einheit auch als "Torr" bezeichnet.
Es gilt folgende Umrechnungsformel: 1 atm = 760 Torr = 760 mm Hg = 1013,25 mbar = 1013,25 hPa oder umgekehrt: 1 Pa entspricht ungefähr 9,8692*10-6 atm.
Da 760 mm Hg bzw. 1 atm als der mittlere Luftdruck auf Meereshöhe (Normal-Luftdruck) definiert wurde, gilt entsprechend der krumme Wert von 1013,25 mbar bzw. 1013,25 hPa heute als Normal-Luftdruck. Dementsprechend ist dieser Wert auf unseren Barometern genau in der Mitte der Skala angeordnet.
 Das nebenstehende Bild zeigt die Skala eines Yacht-Barometers, das
den Luftdruck sowohl in internationalen hPA (= mbar) als auch (innere Skala)
in Torr bzw. mm Hg anzeigt.
Das nebenstehende Bild zeigt die Skala eines Yacht-Barometers, das
den Luftdruck sowohl in internationalen hPA (= mbar) als auch (innere Skala)
in Torr bzw. mm Hg anzeigt.
Nebenbei bemerkt: Die bis 1977 gültige Einheit "Technische Atmosphäre" (at) bezog sich nicht nicht auf den Druck der Luft als den durch die Gewichtskraft der Erdatmosphäre verursachten Druck, sondern auf die Größe des Drucks, die 10 Meter Wassersäule verursacht. Diese Einheit gab es zudem in verschiedenen Ausprägungen. Den Älteren unter uns Chiemsee-Seglern dürfte die Einheit "atü" (Suffix "ü" für "Überdruck") noch von den früheren Reifendruckfüllgeräten an den Tankstellen in Erinnerung sein. Wie auch die US-amerikanische Einheit PSI spielte sie bei Barometern aber nie eine wirkliche Rolle.
Die englische Barometer-Skala
England (und später das vereinigte Königreich) hat als eine der führenden Seefahrer-Nationen schon vor Jahrhunderten seine eigenen nautischen Maßeinheiten zum Standard geführt. Deshalb rechnen wir Segler auch heute noch in Seemeilen und Knoten.
Es war auch ein Engländer, der Meteorologe William Napier Shaw, der 1909 das Bar einführte. Englische Standards behaupten sich gegenüber neueren internationalen Standards oft besonders lange. Gerade auch bei physikalischen Einheiten gehörten die Briten oft zu den Letzten, die ihre nationalen Einheiten den internationalen Standards anpassten. Beispielsweise ist das Zoll (Inch) auch heute noch ein de-facto-Standard weltweit.
 Mit der Einführung des Bars in England bzw. im Vereinigten Königreich (UK)
wurde dort der Wert von 1 Bar bzw. 1.000 mbar als Normal-Luftdruck festgelegt.
Umrechnung:
1.000 mbar = 1.000 hPa = 750 Torr = 750 mm Hg.
Mit der Einführung des Bars in England bzw. im Vereinigten Königreich (UK)
wurde dort der Wert von 1 Bar bzw. 1.000 mbar als Normal-Luftdruck festgelegt.
Umrechnung:
1.000 mbar = 1.000 hPa = 750 Torr = 750 mm Hg.
Daher ist auf englischen Barometern bzw. auf Barometern mit englischer Skala der Wert 1.000 mbar bzw. 750 mm Hg (= 750 Torr) der Mittelwert und gilt als Referenz für die Angabe "Veränderlich" (engl.: "Change"). Siehe das Bild rechts.
Außerdem nutzen England bzw. das Vereinigte Königreich immer noch die eigenen Maßeinheiten für die physikalische Länge (Inch, Yard).
 Das nächste Foto rechts zeigt ein Barometer des renommierten Herstellers
J. Gischard Nachf., Hamburg, aus den frühen 1930er-Jahren (Serie 1651). Hier
in einer Ausführung für Kunden im
Vereinigten Königreich sowie für Freunde und Sammler
von englischen Instrumenten. Ich selber kannte die Skala nicht, als ich
dieses Barometer in die Finger bekam. Das Ergebnis meiner Recherche
war: Die Skaleneinteilung ist in inch (Zoll) ausgeführt. Und zwar nach dem
alten Standard der Quecksilber-Barometer (s.o.), deren Skala in Millimeter
Quecksilbersäule oder eben in englischen Inch Hg ausgeführt war.
Auch hier liegt der "Veränderlich"-Punkt gemäß dem englischen System nicht bei
den internationalen 760 mm Hg (= 1013,25 hPa), sondern bei 750 mm Hg = 29,53 Inch,
was wiederum 1.000 hPa entspricht.
Das nächste Foto rechts zeigt ein Barometer des renommierten Herstellers
J. Gischard Nachf., Hamburg, aus den frühen 1930er-Jahren (Serie 1651). Hier
in einer Ausführung für Kunden im
Vereinigten Königreich sowie für Freunde und Sammler
von englischen Instrumenten. Ich selber kannte die Skala nicht, als ich
dieses Barometer in die Finger bekam. Das Ergebnis meiner Recherche
war: Die Skaleneinteilung ist in inch (Zoll) ausgeführt. Und zwar nach dem
alten Standard der Quecksilber-Barometer (s.o.), deren Skala in Millimeter
Quecksilbersäule oder eben in englischen Inch Hg ausgeführt war.
Auch hier liegt der "Veränderlich"-Punkt gemäß dem englischen System nicht bei
den internationalen 760 mm Hg (= 1013,25 hPa), sondern bei 750 mm Hg = 29,53 Inch,
was wiederum 1.000 hPa entspricht.
Übrigens: auch englische Wetterkarten sind anders: bei uns werden die Isobaren in 5-hPa-Abständen eingezeichnet, in englischen Wetterkarten dagegen im Abstand von je 4 hPa.
Auf Meereshöhe reduzierter Luftdruck
Zurück zur Theorie. Nehmen wir einmal an, wir haben ein auf Meereshöhe kalibriertes Barometer an Bord. Der Chiemsee liegt aber auf einer Höhe von ca. 518,2 Metern, daher zeigt dieses Barometer hier einen geringeren Luftdruck an als die Wetterkarte. Das Barometer hat ja keine Ahnung, wo und in welcher Höhe es gerade ist und zeigt einfach mehr oder weniger den absoluten Druck am jeweiligen Ort an. Mit den Fehlern, die durch die individuelle Kalibrierung bedingt sind. In der Wetterkarte sind die Isobaren dagegen mit dem relativen Luftdruck eingezeichnet bzw. der Luftdruck der Messstellen (hier: Messstelle Chieming) mit dem relativen Luftdruck angegeben. Die Frage ist nun, wie übersetzen wir den angezeigten, absoluten Luftdruck in den relativen Luftdruck? Also in den auf Meereshöhe "übersetzten" Luftdruck, der in der Physik "reduzierter" Luftdruck genannt wird. (Obwohl er vom Betrag her größer ist.)
Dazu gibt es verschiedene Methoden. Die erste Möglichkeit ist die Anwendung einer mathematischen Formel. In der Physik-Literatur finden sich gleich mehrere hierzu. Aber Vorsicht! Physikalische Modelle und die daraus resultierenden Berechnungs-Formeln (hier: Reduktionsformeln) sind nie exakt, allenfalls eine mehr oder weniger gute Näherung.
Wir suchen also eine mathematische Funktion für die Umrechnung zwischen
dem gemessenen absoluten Luftdruck in H=518,2 m und dem relativen Luftdruck (Meereshöhe).
Diese mathematische Funktion kann grundsätzlich in 2 Formen
vorkommen: entweder wird vom relativen Luftdruck ein von der Höhe (und idealerweise von
den anderen Parametern abhängiger) Betrag X abgezogen, in der Form:
p(H) = p0 - X
bzw. umgekehrt: p0 = p(H) + X.
mit H: Höhe über NN
p0: relativer Luftdruck
X: Wert für die jeweilige Höhe H
Wobei X auch als f(H) ausgedrückt werden kann.
Für den Physiker (Meteorologen, Ingenieur, Wissenschaftler) ist das nun aber nicht wirklich korrekt, sondern nur eine grobe Näherung (für uns Segler aber dennoch brauchbar, wie wir später noch sehen werden). Denn bei der mathematischen Beschreibung und Herleitung physikalischer Sachverhalte ergibt sich üblicherweise ein mathematischer Faktor, mit dem Größen bei Änderung der Randbedingungen multipliziert werden.
Genau so ist es auch hier. Bei der Berechnung des Luftdrucks bei veränderlichen
Randbedingungen ergeben sich aus der Theorie die sog. "Höhenformeln",
die den Luftdruck in einer bestimmten Höhe H mit dem Luftdruck
auf Meereshöhe (relativer Luftdruck)
über einen mathematischen Faktor verknüpfen.
Im einfachsten Fall ergibt sich dabei eine Formel nach diesem Schema:
p0 = p(H gemessen) * f(H)
mit H: Höhe über NN
p0: relativer Luftdruck
Der Luftdruck hängt allerdings nicht nur vom absoluten Höhenunterschied
ab, sondern zusätzlich von weiteren Parametern wie der Temperatur T.
Daher ist eine Formel in dieser Form gesucht:
p(H) = p0 * f(T,H) bzw. umgekehrt.
Dabei ist die Temperatur in der Theorie selber abhängig von der lokalen Höhe (je höher, desto kälter). Bei unserem Spezialfall Chiemsee ist es allerdings völlig anders, denn im Chiemgau ist es im Sommer nicht kälter, sondern deutlich wärmer als an unseren Küsten. Außerdem herrscht hier oft ein völlig anderes Wetter als im Rest der Wetterkarte. (Bei einer Wanderung auf die Kampenwand oder den Hochgern stimmt die Theorie dann aber doch meistens wieder. Aber eben nur bei einem Höhenunterschied zwischen 520 m und dem Gipfel).
Eigentlich könnten wir das Kapitel "Theorie" daher an dieser Stelle beenden. Aber da in der Literatur und insbesondere in den Wikipedia-Artikeln einige Fehler stecken (insbesondere bei den Bezeichnungen der verschiedenen Höhenformeln), stellen wir die relevanten Formeln doch vor und berechnen jeweils ein paar typische Werte für den reduzierten Luftdruck.
Mit ein wenig Mathematik ergeben sich aus den physikalischen Grundlagen die
sog. Höhenformeln. Bei der Herleitung dieser Formeln werden üblicherweise
verschiedene Annahmen
zur Vereinfachung vorausgesetzt. Die beiden ersten Vereinfachungen betreffen
den Verlauf der Temperatur über die Höhe. Eigentlich ist die Abnahme der
Temperatur nichtlinear. Und wegen der wechselseitigen Abhängigkeiten
von den anderen Größen
wäre statt einfacher Differentialgleichungen ein komplexes
Gleichungssystem zu lösen. Die entscheidenden Vereinfachungen sind daher:
- Annahme: die Temperatur ist konstant, unabhängig von der absoluten Höhe.
- Annahme: die Temperatur nimmt linear ab. Hier wird ein empirischer (also aus der praktischen Erfahrung gewonnener) Temperaturgradient angewendet.
- Als weitere Vereinfachung werden zusätzlich die Parameter der sog. Normatmosphäre (Normbedingungen) angenommen.
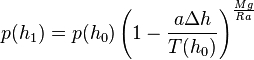
mit a: der Betrag des vertikalen atmosphärischen Temperaturgradienten
Die Lektüre des u.g. Artikels hierzu und eigene Berechnungen kann man sich allerdings sparen, denn für den Zeitraum der Segelsaison am Chiemsee hat sich ein mittlerer Temperaturgradient von 0,65 K pro 100 m als allgemeiner Erfahrungswert etabliert. Damit nimmt der Exponent Mg/Ra für unsere Höhen zwischen NN und den Alpengipfeln den Wert 5,255 an. Und damit ergibt sich die folgende Formel, die in der deutschsprachigen Literatur als die Barometrische Höhenformel bezeichnet wird:
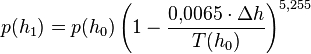
Mit dieser Formel kann man nun z.B. eine Excel-Tabelle erstellen, die für verschiedene angenommene oder gemeldete T(h0) die Reduktion des in der Höhe H gemessenen absoluten Luftdrucks berechnet. Oder präziser formuliert: den auf Meereshöhe reduzierten Luftdruck. Oder umgangssprachlich formuliert: den relativen Luftdruck.
Diese Berechnung kann man natürlich auch umgekehrt durchführen. In der folgenden Tabelle haben wir den theoretischen Luftdruck auf Chiemsee-Höhe berechnet. Gegebene Voraussetzung: p(h0) = Normaldruck,
Parameter: verschiedene T(h0):
| p(h0) [hPa] |
T(h0) [° C] |
T(h0) [K] |
H [m] |
p(H) [hPa] |
Delta p [hPa] |
|---|---|---|---|---|---|
| 1013,25 | 10 | 283,15 | 518,2 | 951,49 | 61,76 |
| 1013,25 | 15 | 288,15 | 518,2 | 952,54 | 60,71 |
| 1013,25 | 20 | 293,15 | 518,2 | 953,55 | 59,70 |
| 1013,25 | 25 | 298,15 | 518,2 | 954,52 | 58,73 |
| 1000 | 10 | 283,15 | 518,2 | 939,05 | 60,95 |
| 1000 | 15 | 288,15 | 518,2 | 940,08 | 59,92 |
| 1000 | 20 | 293,15 | 518,2 | 941,08 | 58,92 |
| 1000 | 25 | 298,15 | 518,2 | 942,04 | 57,96 |
Anm.: Im Internet gibt es auch Online-Rechner. Die Seite, die in mehreren
Wikipedia-Artikeln verlinkt ist, berechnet allerdings andere Werte. Das dort benutzte
Skript benutzt einen etwas veränderten Algorithmus:
Online-Rechner Barometrische Höhenformel
Zur Erinnerung: wir suchen eine Formel bzw. einen Korrekturfaktor, um den absoluten
Luftdruck in den auf Meereshöhe reduzierten Luftdruck umzurechnen. Am einfachsten
ist es, wenn wir einen Differenzwert zum angezeigten Wert addieren können.
Genau deshalb ist die Tabelle um die Spalte mit der Differenz zwischen den
beiden Luftdruck-Werten ergänzt (Delta p).
Wie man an den Beispieldaten sehen kann, ist diese Differenz nicht konstant,
sondern ändert sich ebenfalls mit der Temperatur. Man bräuchte, um den Fehler
zu minimieren, eine temperaturkompensierte Skala. Und wegen der exponentiell
verlaufenden Abnahme müsste die Skala obendrein gespreizt werden.
Wir sehen: ein fehlerfreies kalibriertes "Chiemsee-Barometer" kann es nicht geben.
Aber wir wissen ja inzwischen, dass wegen des im Chiemgau völlig anderen
lokalen Wetters (und der im Sommer höheren Temperaturen als am Meer)
die Anwendung der Barometrischen Höhenformel ohnehin fehlerhaft ist. Insofern
brauchen wir uns um diese Kalibrierungs-Ungenauigkeiten keine Gedanken machen.
Bei der weiteren Vereinfachung nach c) entfallen diese Fehler dann auch zum Teil.
In unserer Kalibrierungs-Aufgabe geht es uns ja
ausschließlich um den berechneten Luftdruck auf Meereshöhe. Also nehmen wir als
Voraussetzungen an:
- p(h0) = 1013,25 hPa
- T(h0) = 15° C
- lineare Abnahme der Temperatur mit o.g. Temperaturgradienten
1013,25 hPa ist der Normal-Luftdruck in Meereshöhe. Und die Temperatur von 15° C ist das langjährige Mittel der Temperatur in Meereshöhe (genauer: in unseren Breiten). Warum aber nimmt man weltweit genau diese Werte als Parameter für unsere Aufgabe?
Antwort: Mit dem Normal-Luftdruck in Meereshöhe befinden wir uns genau in der Mitte der Barometerskala. Zu beiden Seiten hin treten damit bei allen Barometern die gleichen Fehler auf, wenn sie auf die Anzeige des relativen Luftdrucks kalibriert werden bzw. die Werte umgerechnet werden. Die Festlegung auf die mittlere Temperatur (Jahresmittel) verringert die Ungenauigkeiten ebenfalls. Es gibt aber einen noch wichtigeren Grund:
Mit der einheitlichen Festlegung auf diese Werte werden alle Barometer weltweit vergleichbar. (Dasselbe gilt auch für die Höhenmesser (Altimeter) in Flugzeugen.)
Mit diesen normierten Parameterwerten wird nämlich aus der Barometrischen Höhenformel die sog. Internationale Höhenformel:
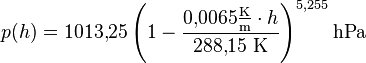
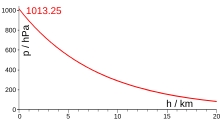 Die Grafik rechts zeigt den Verlauf. (Genau genommen
nur korrekt in der linken Hälfte, unterhalb ca. 10 km Höhe.)
Die Grafik rechts zeigt den Verlauf. (Genau genommen
nur korrekt in der linken Hälfte, unterhalb ca. 10 km Höhe.)Für den Chiemsee ergibt sich hier ein Wert von 952,54 hPa als Normal-Luftdruck, bei einer Temperatur von 15° C auf Meereshöhe. Und eine Differenz zwischen den beiden Luftdruck-Werten von 60,71 hPa.
Diese speziellen Parameterwerte gelten in Deutschland als Normbedingungen (auch Normalbedingungen). Sie sind in der DIN 1343 festgeschrieben. Die Beschreibung der erdnahen Atmosphäre unter der Annahme dieser Normbedingungen wird in Deutschland als Normatmosphäre bezeichnet . Sie gelten auch international als Standard und die entsprechend vereinfachte Beschreibung der erdnahen Atmosphäre wird in der internationalen Norm ISO 2533 als International Standard Atmosphere (ISA) spezifiziert.
Anm.: Statt Normatmosphäre wird im Deutschen auch der
Begriff Standardatmosphäre
verwendet. Dieser meint oft das selbe, ist aber nicht offiziell.
Manchmal gibt es aber einen Unterschied: In der Literatur,
und dementsprechend auch bei Wikipedia, wird
die Bezeichnung Standardatmosphäre manchmal auch für eine vereinfachte
Beschreibung der erdnahen Atmosphäre verwendet, die zwar
weitgehend der Normatmosphäre
entspricht, allerdings nicht die Festlegung der Normtemperatur
auf 15° C enthält. Mit dieser Standardatmosphäre ist
dann meistens das allgemeinere Modell mit der linearen
Temperatur-Abnahme mit o.g. Temperaturkoeffizienten gemeint.
Aufpassen muss man auch bei den Begriffen Normbedingungen und
Standardbedingungen. Die Normbedingungen sind
verbindlich festgelegt, z.B. für Luftdruck und Temperatur in der DIN 1343.
In den verschiedenen wissenschaftlichen und technischen Fachbereichen werden
dagegen oft hiervon abweichende, sog. Standardbedingungen verwendet. Relevant
ist das z.B. für den sog. Standard-Luftdruck, der oft auf 1.000 mbar festgelegt
wird. Der Grund ist, dass man mit diesem Wert einfacher rechnen kann.
Und in Großbrítannien wird oft noch mit der alten Standard Atmosphere
gearbeitet, die ebenfalls einen "normalen" Luftdruck von 1.000 hPa in Meereshöhe
definiert. Diese entspricht also weder unserer umgangssprachlichen
Standardatmosphäre noch der International Standard Atmosphere (ISA).
Sie benutzt aber unsere Standardbedingungen. Alles klar?
Diese begriffliche Verwirrung hat ihre Ursache oft in der Übersetzung
vom Englischen ins Deutsche. Für das englische Standard wird oft
leichtfertig der deutsche
Begriff Standard anstatt Norm verwendet.
Im wissenschaftlichen und technischen
Bereich ist das eben oft nicht korrekt.
Der Sonderfall nach der vereinfachten Annahme nach a) spielt in der Meteorologie dann eine Rolle, wenn es um spezielle Reduktionsformeln geht. Hierbei wird eine mittlere Temperatur als konstant angenommen. Das wird manchmal auch anders ausgedrückt: die Temperatur auf halber Höhe. Das ist dann i.d.R. aber dasselbe, wenn diese mittlere Temperatur wiederum mit Hilfe des o.g. linearen, mittleren Temperaturgradienten ermittelt wird. Bevor wir uns im nächsten Kapitel auf die praktischen Näherungen für den Chiemsee konzentrieren, schauen wir uns noch eine solche Berechnungs-Methode an. Die bisherigen Formeln basieren ja auf stark vereinfachten Modellen, die deshalb auch vor allem in der Schul-Literatur vorkommen. Tatsächlich ist die Abnahme des Luftdrucks mit der Höhe aber wesentlich komplexer. Der Luftdruck hängt außer von der absoluten Höhe noch von vielen weiteren Parametern ab. Dazu gehören:
- die Temperatur, die mit zunehmender Höhe rein mathematisch nichtlinear abnimmt und in der Realität vom lokalen Wetter bestimmt wird
- die Luftdichte, die mit zunehmender Höhe nichtlinear abnimmt
- die Luftfeuchtigkeit, die das Molekulargewicht eines bestimmten Luftvolumens verändert
- über die Breitengrade sich die Gravitation verändert
- die Luftsäule zur Berechnung keine Zylinderform hat, sondern einem stumpfen Kegel entspricht
Anmerkung zum Parameter Luftfeuchtigkeit (auch Luftfeuchte genannt):
Die Luftfeuchte unter 100 % können wir nicht sehen, nur messen. Erst unterhalb der
sog. Taupunkt-Temperatur (oder kurz Taupunkt)
wird der Wasserdampf der gesättigten Luft (100 % Luftfeuchte) für uns durch
die Kondensation sichtbar. Als Tau, Nebel oder Wolken. (Am deutlichsten als Cumulus-Wolken.)
Und nicht nur die Regatta-Segler unter uns wissen: Wolken bringen Wind.
Wir wissen ja, dass Wind durch Luftdruck-Unterschiede entsteht (Ausgleich
Hoch --> Tief, mit den entsprechenden Rotations-Effekten). Nun haben wir gerade
gelesen, dass der Luftdruck auch von der Luftfeuchte abhängt. Damit können
wir ein (sehr) einfaches physikalisches Modell erstellen: Unter der Wolke herrscht ein
höherer Luftdruck als neben der Wolke und daraus resultiert der bodennahe Segelwind.
Ganz so einfach ist es aber letztlich doch nicht. Denn der Luftdruck ist ja
der resultierende Druck der einzelnen Luftsäulen mit Wolken oder ohne Wolken.
Und in jeder dieser Luftsäulen muss genau genommen das Integral über die Verteilung
der Luftfeuchte (und damit über das Molekulargewicht der Luft) berechnet werden.
Es kommen in diesem Integral natürlich auch alle Anteile der jeweiligen Luftfeuchte
unter 100 % vor. Die wir nicht sehen können. Die aber das einfache Modell
"Wolke / keine Wolke" durcheinander bringen.
Außerdem hängen alle Größen auch von der lokalen Temperatur ab. Unter einer Wolke
ist die Luft-Temperatur geringer als in derselben Höhe neben der Wolke. Das verschiebt
wiederum den Taupunkt. Wenn es sich aber um eine Aufwärtsbewegung der Luft aufgrund der
unterschiedlichen Erwärmung von Chiemsee und dem Land darum herum handelt, also um
reine Thermik, dann kommen zu den einfachen Regeln weitere Effekte hinzu.
Entscheidende Parameter hängen wiederum von anderen Parametern und deren
Einfluss auf die Berechnung mit jenen Parametern ab. Es handelt sich hier also
um ein hochkomplexes System aus sich verändernden, voneinander abhängigen Parametern
und rekursiven Berechnungsformeln. Dieses System erfodert daher mehrschichtige iterative
Lösungsansätze. Das sprengt natürlich den Rahmen dieses Artikels und wir überlassen
diese komplexe Thematik lieber den Wetter-Profis. Zollen wir lieber Hochachtung
den erfolgreichen Regatta-Seglern, die solche Konstellationen zu nutzen wissen.
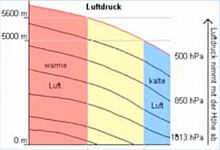 Im Bild rechts ist ein komplexes Berechnungsmodell dargestellt,
wie es von den Meteorologen im Alltags-Geschäft benutzt wird.
Anders als in den "einfachen" Beschreibungen über 2 Koordinaten ist hier der
Verlauf des Luftdrucks in Form von Isobaren dargestellt. Und zwar in
gleichzeitiger Abhängigkeit von den Parametern Höhe und Temperatur.
Man sieht trotz der anderen Darstellungsweise, dass der Verlauf p(h) nicht
einer einfachen exponentiellen Abnahme entspricht.
Im Bild rechts ist ein komplexes Berechnungsmodell dargestellt,
wie es von den Meteorologen im Alltags-Geschäft benutzt wird.
Anders als in den "einfachen" Beschreibungen über 2 Koordinaten ist hier der
Verlauf des Luftdrucks in Form von Isobaren dargestellt. Und zwar in
gleichzeitiger Abhängigkeit von den Parametern Höhe und Temperatur.
Man sieht trotz der anderen Darstellungsweise, dass der Verlauf p(h) nicht
einer einfachen exponentiellen Abnahme entspricht.
Eine erwähnenswerte Berechnungsformel, in der die tatsächliche Beschaffenheit
der Luft und der lokalen Randbedingungen wenigstens teilweise berücksichtigt werden,
ist die vom DWD empfohlene Reduktionsformel:

mit a: vertikaler Temperaturgradient, hier die schon bekannten 0,0065 K/m
T(h): gemessene absolute Temperatur in der Höhe h [K]
E: Dampfdruck des Wasserdampfanteils [hPa]
Ch: Beiwert zu E zur Berücksichtigung der mittleren
Dampfdruckänderung mit der Höhe
(genauer: mit der Temperaturänderung mit der Höhe), hier aber als konstanter Mittelwert
= 0,12 K/hPa
Diese Formel ist sicherlich sinnvoll zur Reduktion der Messwerte der einzelnen
Wetterstationen zur Erstellung der Wetterkarten. Bei den Profi-Messstationen
werden die Daten der Luftfeuchte auch entsprechend erfasst. Bei den Hobby-Messstationen
ist dies jedoch oft nicht der Fall. Die Luftdruck-Angaben der verschiedenen Messstationen
am Chiemsee sind daher erst einmal mit Vorsicht zu verwenden. (Das wäre doch
eine schöne Praxis-Arbeit, die einzelnen Stationen einmal auf ihre reale
Praxistauglichkeit bzw. korrekte Kalibrierung hin zu überprüfen. Aber bitte erst
den Artikel zu Ende lesen.)
So weit zu den "Schul-Methoden" zur rechnerischen Reduktion. Und
für die Praxis empfehlen wir im nächsten Kapitel noch andere Methoden,
um das Bordbarometer richtig zu kalibrieren.
Aber zunächst stellen wir zum Abschluss des Kapitels "Theorie" noch die Näherungs-Formel vor, die auch von den Wetterdiensten als praxistaugliche Näherung genannt wird.
Sie ist die Faustformel, die
mathematisch die Linearisierung der besseren Reduktionsformeln darstellt,
den Einfluss der Temperatur nur über die gemittelten Erfahrungswerte
berücksichtigt, und sie lautet:
Alle 8 m über NN nimmt der Luftdruck um 1 hPA ab.
(Mit zunehmender Höhe nimmt der Betrag dieser Höhenstufe zu,
ab ca. 5.000 m sind es schon 16 m. Für die Höhen unserer Binnenseen
ist diese Formel daher ohne Korrektur absolut brauchbar.)
Für den Chiemsee ergibt sich hieraus für den lokalen normalen
Luftdruck (genau: für den lokalen statischen Luftdruck auf 518,2 m geografischer
Höhe bei Normbedingungen):
1013,25 - (518,2 / 8) = 948,475 hPa. Und damit eine Differenz von
64,775 hPa.
Und umgekehrt wird ein lokaler Luftdruck von 950,0 hPa mit der Faustformel zu einem relativen Luftdruck von 1014,775 hPa. Die absolute Differenz von 64,775 hPa bleibt dieselbe, trotz der erhöhten Absolut-Werte.
Fazit: Am selben Ort gilt nach der Faustformel immer derselbe Differenzwert, unabhängig von den absoluten Luftdruckwerten.
Wir merken uns diese Werte, wir werden sie im Folgenden noch brauchen.
Meteorologische Besonderheiten speziell am Chiemsee
Im Laufe des Artikels wurde bereits erwähnt, dass der Chiemgau ein gegenüber den meisten anderen Regionen besonderes meteorolgisches Verhalten hat. Dazu gehört insbesondere eine im Sommer oft über der deutschlandweiten Durchschnitts-Temperatur liegende lokale Temperatur. Das alleine schon macht die Anwendung der barometrischen Höhenformeln ungenau.
Speziell für den Chiemsee kommen weitere für den Luftdruck relevante Besonderheiten dazu. Das sind die Lage direkt an den Alpen, der Einfluss von Fön-Wetterlagen, die Grenze zwischen Ost- und West-Wetterlagen, und insbesondere die Größe der Wasserfläche. Diese bewirkt bekanntlich ausgeprägte Land- und Seewind- Effekte, die letztlich auf Luftdruck-Unterschieden beruhen. Bei Sonneneinstrahlung verstärken sich diese lokalen Effekte. Daher ist der absolute Luftdruck am Chiemsee selten seeweit gleich. Erfahrene Regatta-Segler wissen um den Einfluss von einzelnen Wolken auf den lokalen Wind, also letztlich wieder den Einfluss auf den lokalen Luftdruck. Der jeweilige lokale Luftdruck ist am Chiemsee also eine zeitlich und örtlich sehr eingegrenzte Momentaufnahme.
Es ist am Chiemsee außerdem nicht ungewöhnlich, dass sich der Luftdruck innerhalb von 24 Std. um mehr als 20 hPa ändert. Der nachfolgende Screenshot zeigt einen entsprechenden wechselhaften Verlauf (Wetterstation Chieming, 02/2017).
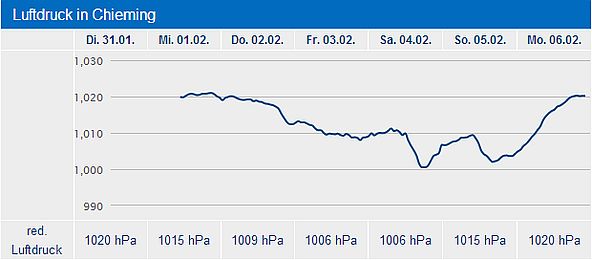
Bei der Kalibrierung von Barometern am Chiemsee unter Verwendung der Messdaten der Wetterstation Chieming ist es demnach wichtig, immer den aktuellen Messwert zu benutzen. Und möglichst nahe der Messstation zu sein. Dazu kann man entweder nach Chieming segeln oder das Bordbarometer bei einem Landausflug nach Chieming mitnehmen.
Hinweis: Die angegebene geografische Höhe der Wetterstation Chieming ist 553 m. Das sind also ca. 35 m über dem Seespiegel bzw. ca. 34 m über der Höhe unserer Schiffs-Barometer. Aus dieser Höhen-Differenz ergibt sich eine durchaus relevante Abweichung des lokalen statischen Luftdrucks. Die korrekte Ermittlung kann mit Hilfe der o.g. Formeln rechnerisch aber nur ungenau ermittelt werden, da die Temperaturen an Land und auf dem See sich über die Tageszeit unterschiedlich entwickeln und damit auch die Entwicklung des Luftdrucks unterschiedlich verläuft. (Das kennen wir Segler ja bereits vom Effekt Landwind-Seewind tagsüber und nachts, abhängig insbesondere von der Sonneneinstrahlung.) Eine brauchbare Näherung ist immer die Verwendung der Faustformel, damit ergibt sich ein Luftdruck-Unterschied (lokaler statischer Luftdruck) von 4,35 hPa zwischen See-Oberfläche und der Messstation Chieming.
Führen wir nun eine zweite Rechnung mit den vorhin benutzten Werten durch. Bei 950,0 hPa (statischer Luftdruck) auf Seehöhe ergibt sich ein errechneter Wert von 950,0 - 4,35 = 945,65 hPa (statischer Luftdruck) auf 553 m Höhe. Diesen Wert reduzieren wir jetzt auf NN: 945,65 +(553/8) = 1014,775 hPa. Das ist derselbe reduzierte Luftdruck wie vorhin für Seehöhe errechnet. Lediglich die Differenz zwischen statischem und reduziertem Luftdruck ist mit 69,125 hPa etwas größer, und zwar um genau die 4,35 hPa, die aus der höhenbedingten Abnahme des Luftdrucks resultiert. Wie vorhin lässt sich diese Rechnung auch umgekehrt durchführen.
Fazit: Wir können den statischen Luftdruck einer Messstation auf einen anderen Ort mit unterschiedlicher Höhe umrechnen. Die Reduktion dieses Luftdrucks wiederum ergibt denselben relativen Luftdruck wie am Ort der Messung.
Für das folgende Kapitel, in dem es um die praktische Anwendung geht, sind aber noch weitere Voraussetzungen bzw. Einschränkungen notwendig:
- Der relative Luftdruck schließt den Einfluss von Höhenunterschieden weitgehend aus.
- Die besondere meteorologische Situation im Chiemgau bewirkt allenfalls "Dellen" in der Isobarenkarte.
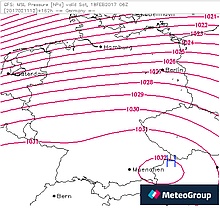 Diese "Dellen" haben eine eine Auswirkung zwischen 0 und +1 hPa. Siehe dazu die
Isobarenkarte im Bild rechts. Hier liegt der relative Luftdruck in der Region
Chiemgau-Salzburg um 1 hPa höher als in der Umgebung. Dies ist statistisch
als Ausnahme-Situation anzusehen.
Diese "Dellen" haben eine eine Auswirkung zwischen 0 und +1 hPa. Siehe dazu die
Isobarenkarte im Bild rechts. Hier liegt der relative Luftdruck in der Region
Chiemgau-Salzburg um 1 hPa höher als in der Umgebung. Dies ist statistisch
als Ausnahme-Situation anzusehen.
- Der Chiemsee selber kann lokale Abweichungen aufweisen.
- Diese Abweichungen sind für den Vorgang der Barometer-Kalibrierung ohne Auswirkung, wenn wir uns dafür in unmittelbarer Nähe der Referenz-Wetterstation befinden. Wir beziehen uns hierbei explizit auf die Wetterstation Chieming.
- Lokale Wetterentwicklungen (z.B. lokale Wärmegewitter) verursachen grundsätzlich extreme Abweichungen von den eigentlich geltenden lokalen Luftdruck-Werten. Diese Extrem-Bedingungen müssen wir daher für unsere Betrachtungen und für die Praxis-Anwendung ausblenden.
- Für die folgende Praxis-Anwendung gilt zusammenfassend die folgende Annahme: Bei normalen Wetterdingungen und idealerweise Normbedingungen gilt: Der relative Luftdruck am Ort der Wetterstation Chieming und dem Standort direkt davor (z.B. dem Hafen Unterhochstätt) ist identisch.
Barometer-Praxis (nicht nur) für den Chiemsee
Wer direkt hierher gesprungen ist, hat das Wesentliche noch nicht versäumt. Denn obwohl die Theorie der Reduktion interessant ist, geht es hier letztlich doch immer nur um die Praxis-Anleitung: wie kalibriere ich mein Bord-Barometer korrekt auf den relativen Luftdruck für den Chiemsee? (Bzw. für meinen aktuellen Standort.) Oder anders ausgedrückt: zeigt mein Bord-Barometer den richtigen Luftdruck an?
 Für die Praxis-Tipps gehen wir wieder von einer Annahme aus.
Nämlich der Annahme, dass die renommierten Wetterdienste
in der Lage sind, die beste Reduktion vom lokalen zum relativen Luftdruck
zu liefern. Sehen wir uns also eine reale Stationsmeldung der Messstelle Chieming
an 3) 4).
Für die Praxis-Tipps gehen wir wieder von einer Annahme aus.
Nämlich der Annahme, dass die renommierten Wetterdienste
in der Lage sind, die beste Reduktion vom lokalen zum relativen Luftdruck
zu liefern. Sehen wir uns also eine reale Stationsmeldung der Messstelle Chieming
an 3) 4).
Der Screenshot rechts zeigt die Daten der Messstation Chieming vom 17.08.2015, 21:00 Uhr.
An diesem Abend lag die Temperatur an Nord- und Ostsee ebenfalls zwischen 15° C
und 20° C. Der relative Luftdruck betrug 1013,3 hPa, damit liegen
ziemlich genau die oben beschriebenen Normbedingungen vor. Und damit erhalten wir
ein fast ideales Ergebnis der Reduktionsaufgabe von den Profis.
Der lokale Luftdruck in 553 m Höhe betrug 950,0 hPa, der reduzierte Luftdruck
bei T(h0) ca. 15° C wird auf 1013,3 hPa berechnet.
Das entspricht also einer Differenz unter (fast) Normbedingungen
von 63,3 hPa.
Wenn wir diese Werte mit den Ergebnissen der oben vorgestellten Formeln vergleichen, dann stellen wir fest: die beiden Höhenformeln liegen relativ weit daneben. Aber auch die Faustformel trifft mit der örtlichen Differenz (s.o.) von ca. 69,1 hPa den "richtigen" Wert nicht.
Welchen Schluss ziehen wir nun daraus im Hinblick auf die beste Methode zur korrekten Kalibrierung unserer Bord-Barometer?
Die einzig richtige Antwort ist: Wenn möglich, dann den relativen Luftdruck der nächstliegenden offiziellen Wetterstation benutzen.
Als Fazit und als Praxistipps halten wir fest:
- Die sog. Reduktionsformeln geben eine erste Näherung der hochkomplexen physikalischen Zusammenhänge wieder. Mehr nicht.
- Eine genauere Berechnung ist mit Hobby-Mitteln und -Methoden nicht machbar.
- Die Wetterlage im Chiemgau (und damit speziell am Chiemsee) ist oft von der deutschlandweiten Großwetterlage verschieden.
- Die sog. Faustformel ist nicht praxistauglicher als die Reduktionsformeln.
- Die Anzeige-Genauigkeit ist bei analogen Instrumenten nicht linear und es gibt Fehler, die u.a. von der Höhe abhängen. Je größer der Zeigerausschlag (d.h., je mehr der aktuelle Luftdruck vom Normluftdruck abweicht), desto größer ist die Abweichung.
- Dieser Fehler ist u.a. von der Höhe abhängig. Am kleinsten ist die Abweichung in der Höhe, für die das Barometer konstruiert wurde. Auf diese Höhe werden die Barometer von den Herstellern kalibriert ("Werks-Einstellung").
- Für Schiffs-Barometer ist die vorgesehene Einsatz-Höhe 0 m (Meeres-Höhe, Normal-Null). Barometer für den stationären Gebrauch werden je nach Hersteller ab Werk auf Höhen zwischen 150 m und 350 m kalibriert.
- Präzisions-Instrumente bieten eine zusätzliche Justier-Möglichkeit zur Kompensation dieser Abweichung (s.u.).
- Die beste Methode für Chiemsee-Segler ist: Segeln Sie an einem passenden Tag (siehe hierzu den Tipp weiter unten) nach Chieming oder Unterhochstätt. Rufen Sie online den aktuellen relativen Luftdruck der Messstation Chieming ab (Links siehe unten.) Justieren Sie Ihr Barometer auf diesen Wert.
- Die zweitbeste Methode: Wenn Ihr Schiff am oder auf dem Chiemsee liegt,
nutzen Sie den vorigen Tipp als ersten Schritt, ohne nach Chieming zu segeln.
Überprüfen Sie das Ergebnis, wenn Sie später einmal nach Chieming segeln. - Benutzen Sie unbedingt nur die Wetterstationen der renommierten Wetterdienste. (Für diesen Artikel waren dies der DWD und die MeteoGroup.) Privat betriebene Wetterstationen sind oft selber nicht richtig kalibriert.
 Je nach Barometer-Art gibt es verschiedene Schrauben, an denen Sie drehen
können. Bei analogen Barometern (Dosenbarometer, Zeiger-Instrumente) sind diese
üblicherweise auf der Rückseite des Geräts zugänglich.
Es ist mindestens eine Stell-Schraube für die Justierung des Anzeigewertes
vorhanden. Anders ausgedrückt: man stellt damit den Zeiger ein. Bessere Instrumente
haben weitere Stell-Schrauben, mit denen man z.B. die Spreizung der Anzeige
einstellen kann (Fehler-Kompensation abhängig von der Höhe und anderen
Parametern). Gerade bei Dosenbarometern, die ja einen definierten Unterdruck
ab Werk haben, ändert sich die Empfindlichkeit mit der Höhe (je höher, desto
geringer der absolute Druck, und damit desto geringer der Druckunterschied
zwischen Luftdruck und Unterdruck in der Dose). Präzisions-Instrumente
haben hierfür eine weitere Stell-Schraube. Die handelsüblichen Schiffs-
Barometer haben jedoch nur die eine Stellschraube zur Einstellung des
Anzeigewerts.
Je nach Barometer-Art gibt es verschiedene Schrauben, an denen Sie drehen
können. Bei analogen Barometern (Dosenbarometer, Zeiger-Instrumente) sind diese
üblicherweise auf der Rückseite des Geräts zugänglich.
Es ist mindestens eine Stell-Schraube für die Justierung des Anzeigewertes
vorhanden. Anders ausgedrückt: man stellt damit den Zeiger ein. Bessere Instrumente
haben weitere Stell-Schrauben, mit denen man z.B. die Spreizung der Anzeige
einstellen kann (Fehler-Kompensation abhängig von der Höhe und anderen
Parametern). Gerade bei Dosenbarometern, die ja einen definierten Unterdruck
ab Werk haben, ändert sich die Empfindlichkeit mit der Höhe (je höher, desto
geringer der absolute Druck, und damit desto geringer der Druckunterschied
zwischen Luftdruck und Unterdruck in der Dose). Präzisions-Instrumente
haben hierfür eine weitere Stell-Schraube. Die handelsüblichen Schiffs-
Barometer haben jedoch nur die eine Stellschraube zur Einstellung des
Anzeigewerts.
Wählen Sie zur Kalibrierung einen Tag mit Normluftdruck aus. Dieser liegt in der Mitte der Skala, damit wird der relative Fehler zu beiden Seiten der Skala hin etwa gleich verteilt. Justieren Sie Anzeige auf den ortsbezogenen reduzierten Luftdruck.
Je größer der Ausschlag zu Hochdruck bzw. Tiefdruck ist, desto größer wird die Abweichung vom richtigen Wert. Dieser Fehler lässt sich bei Instrumenten mit eigener Stellschraube hierfür korrigieren. Das führen Sie (nach der Grund-Einstellung des Normluftdrucks auf den relativen Luftdruck) sinnvollerweise an Tagen mit extremem Luftdruck (also großem Zeigerausschlag) aus.
Die Sensoren der digitalen Geräte reagieren linearer. Diese Geräte haben meist nur eine Justierung für die Einstellung des absoluten Luftdrucks auf den relativen Luftdruck. Je nach Gerät (Armband-Uhr, Digital-Barometer, Messstation, Smartphone, etc.) wird mit Hilfe der Bedienungs-Knöpfe oder über ein Menü der jeweiligen Barometer-App ein absoluter Wert eingestellt oder ein Offset eingestellt. Auch hier gibt es neben den handelsüblichen Einfach-Geräten professionelle Geräte, die sowohl eine Nullpunkt-Kompensation als auch die Einstellung weiterer Offset-Werte anbieten.
Bei den antiken Quecksilber-Barometern verschiebt man einfach die Skala.
[Eine persönliche Anmerkung des Autors: Bitte benutzen Sie zur Einstellung der Werte die Bedienungsanleitung Ihres Geräts. Anfragen an Chiemsee-Segeln.de hierzu können wir nicht beantworten.]
Weitere Praxis-Tipps:
- Wenn Sie mit Ihrem Schiff an einem anderen See liegen, dann rufen Sie den aktuellen Wert für den relativen Luftdruck der nächstgelegenen Messstation ab.
- Derselbe Tipp gilt auch ganz allgemein für die Kalibrierung von Barometern in Haushalten.
- Am besten geeignet für diese Methoden ist ein Tag mit Normluftdruck, an dem das Wetter nicht von nahe gelegenen, lokalen Hochs und Tiefs beeinflusst wird. Ein Tag, an dem möglichst keine Wolkenbildung stattfindet und die Temperaturen deutschlandweit einigermaßen gleich sind. Eine solche Wetterlage herrscht oft im Sommer, wenn das Azorenhoch seine Ausläufer bis nach Mittel-Europa ausstreckt.
- Nur für die Kalibrierung von Barometern in Haushalten, nicht am Chiemsee: Wählen Sie einen Tag mit wenig Wind, denn wenig Wind bedeutet: die Isobaren liegen weit auseinander. Oder anders ausgedrückt: Auch wenn die Entfernung zwischen Ihrem Ort und der nächsten Wetterstation viele Kilometer beträgt, ist dann die Chance auf eine geringe Abweichung am größten.
- Trotz Temperatur-Kompensation der besseren Instrumente bleibt immer noch ein Einfluss der Temperatur auf die korrekte Anzeige. Hängen Sie das Barometer daher sonnengeschützt an einem Platz auf, der sich nicht zu sehr aufheizt. (Also dort, wo auch das Thermometer am besten hängt.)
- Wenn Sie mit Ihrem Schiff zwischen dem Meer und dem Chiemsee (oder einem anderen Binnensee) wechseln, dann merken Sie sich die Umdrehungen der Schraube zur Kalibrierung der Anzeige, die nötig sind zur jeweiligen Anpassung an den örtlichen Wert. So haben Sie beim Wechsel des Reviers zumindest eine erste Näherung an den richtigen Wert bis zur endgültigen Kalibrierung, wie zuvor beschrieben.
- Im Gegensatz zum historischen Segelschiff auf den 7 Weltmeeren ohne Online-Kommunikation können wir auf dem Chiemsee (und in vielen weiteren zivilisierten Gegenden) stets die neuesten Wetter-Vorhersagen digital oder per Radio empfangen. Zur Voraussagung des lokalen Wetters oder zur Warnung vor Unwettern ist das zumindest am Chiemsee die bessere Informations-Quelle als die eigene Interpretation der Luftdruck-Werte des Bord-Barometers.
- Und weil gerade am Chiemsee auch bei schönstem Wetter ein lokales Unwetter in weniger als einer Stunde entstehen kann, ist die Beobachtung des Himmels weitaus wichtiger als die Beobachtung des Barometers.
- Wer den Artikel von hinten gelesen hat: das war die beste Methode, die wichtigsten Aussagen zuerst zu lesen. Wer den Artikel ganz gelesen hat: vielen Dank für Ihr Interesse. Falls Ihnen Fehler aufgefallen sind, oder wenn Sie andere sinnvolle Anmerkungen haben: schreiben Sie mir einfach Ihren Kommentar über das Kontakt-Formular.
Aktuelle Messwerte von Chieming
Links zu aktuellen Messwerten der Wetterstation Chieming:
Nachfolgend eine Auswahl von Websites mit den aktuellen Messwerten von Chieming 4). Update der Messwerte stündlich. Alle Werte zeigen den reduzierten Luftdruck an.
1) Website der MeteoGroup, grafische Darstellung mit dem Verlauf der letzten 5 Tage,
benutzt Javascript. (Die Werte in der letzten Zeile der Luftdruck-Tabelle verstehe
ich nicht, daher habe ich eine entsprechende Anfrage an die Meteomedia GmbH gestellt.):
http://www.wetter24.de/wetterstation/Chieming/10982/
Hinweis: Die Zeitangabe erfolgt hier in UTC (d.h. 1 Std. weniger in der Anzeige).
2) Alternative Seite der MeteoGroup:
http://www.wetter24.de/vorhersage/deutschland/chieming/18226324/
3) Einfache Text-Anzeige des letzten Messwerts:
http://www.br.de/wetter/action/5_tage_prognose.do?plz=10982
4) Einfache Text-Anzeige des letzten Messwerts, manchmal mit Verzögerung:
http://www.wetter.net/cgi-bin/wetter-net3/wetter-stadt-ist.pl?ID=10663&ALIAS=Prien%20am%20Chiemsee&ID2=118570®IO=13&STATION=10982
5) wetteronline.de: Reiter "Verlauf", Auswahl "Luftdruck"
wetteronline.de
6) windfinder gibt den Absolut-Luftdruck an:
windfinder.com
Hinweis: Zum Abruf aktueller Daten per Smartphone oder Wearable bietet die MeteoGroup eine entsprechende App an. Diese gibt es in verschiedenen Ausführungen, siehe http://www.wetter24.de/mehr/wetterapps/
Zum Vergleich: Links zu anderen, privaten Wetterstationen:
Die erste Prüfung ergibt eine Abweichung von ca. -6 hPa:
Wetterstation des CYC in Prien
Die erste Prüfung ergibt eine Abweichung von ca. -5 hPa:
Wetterstation der Stippelwerft in Prien
Das Laden der Daten kann eine Weile dauern.
Bald mehr dazu.
Weiterführende Information und Quellennachweise
Quellen, Literatur
https://de.wikipedia.org/wiki/Barometer
In 2015 teilweise fehlerhafter Artikel:
https://de.wikipedia.org/wiki/Luftdruck
Internationale Höhenformel, Barometrische Höhenformel:
https://de.wikipedia.org/wiki/Barometrische Höhenformel
https://de.wikipedia.org/wiki/Technische Atmosphäre
https://de.wikipedia.org/wiki/Physikalische Atmosphäre
https://de.wikipedia.org/wiki/Atmosphärischer Temperaturgradient
Online-Rechner Barometrische Höhenformel
Online-Rechner Internationale Höhenformel
Aktuelle Messdaten der
DWD-Wetterstation Chieming
(Update: hier hat es Änderungen gegeben, aktuelle Links s.o.)
http://www.yacht.de/yacht_tv/wetter/wetterkunde-serie-teil-2/a6937.html
https://de.wikipedia.org/wiki/Taupunkt
Bildnachweis
1: Produktfoto Schiffs-Barometer und
2: Produktfoto Barograph Wempe Chronometerwerke
Mit freundlicher Genehmigung der Gerhard D. Wempe KG
3: Skizze Einfaches Siphon-Glas von 1883
Wikipedia
4: Goethe-Glas Wikipedia
Creative Commons Attribution-Share Alike 3.0 Unported
5: Grafik Luftdruckverlauf p(h)
WetterWelt GmbH (eigene Ergänzung)
6: Barometerskala siehe 1.
7: Englisches Barometer Wikipedia
Creative Commons Attribution-Share Alike 3.0 Unported
8: Antikes ATCO-Barometer mit alt-englischer Skala, Foto:
Tilo Klesper
9: Grafik: Abnahme des Luftdrucks nach der Internationalen Höhenformel
WetterWelt GmbH
10: Grafik: Abnahme des Luftdrucks im komplexen Modell
WetterWelt GmbH
Alle Bilder mit freundlicher Genehmigung der WetterWelt GmbH
11: Screenshot Stationsmeldung Chieming - war eine Veröffentlichung von wetter.com,
inzwischen hat sich da einiges geändert. Demnächst mehr dazu.
12: Barometer-Rückseite mit Justier-Schrauben, Foto:
Tilo Klesper
Formeln: Alle Formeln stammen aus den Artikeln der Wikipdia, siehe oben.
Anmerkungen
1) Die Einheit "Pascal" für den Druck wurde nach eben diesem Blaire Pascal benannt.
2) Bis 1949 hieß Liège Liége.
3) Bis 2015 wurde die Wetterstation Chieming vom DWD betrieben. Der Screenshot stammt von der damaligen Internet-Seite von www.wetter.com, auf der die Daten des DWD verarbeitet und angezeigt wurden. Heute werden die Messdaten der Wetterstation Chieming exklusiv von der MeteoGroup verarbeitet. Dementsprechend verweisen möglicherweise noch nicht korrigierte Links auf unseren Webseiten heute auf die Seiten der MeteoGroup.
4) Die Wetterstation in Chieming befindet sich natürlich nicht auf Seehöhe, sondern einige Meter höher. Angegeben werden 553 m, das sind 35 m über Seehöhe, und es müssen demnach nach der Faustformel 4,35 hPa Korrektur für den statischen Luftdruck auf Chiemsee-Höhe in die Rechnung eingehen (addiert werden), wenn der Luftdruck auf See-Höhe berechnet werden soll. Der relative Luftdruck ist dann unabhängig von der Berechnungsmethode für beide Bezugsorte (Chieming Wetterstation und Chieming See-Ufer) gleich. Die Angabe von 553 m ist allerdings mehr als die von mir geschätzte Höhe für die Wetterstation, daher bleibt dieser Punkt noch zu klären.
Last Update: 12.02.2017